Confusing lim sup and lim inf

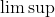
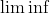
The definitions of and can get super confusing. I h0pe typing it out will help me remember it once and for all.

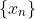
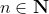
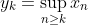
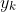
Let be a sequence of real numbers indexed by . Consider the sequence which is formed using the supremums of tails of the original sequence. Observe that is non-increasing (since ``the supremum over a smaller set can only get smaller''). We define.

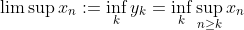
Now if we switch the order of infimum and supremum in the above definition, the new quantity still makes sense (because the sequence of infimums of tails is non-decreasing). It is natural to define .

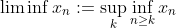
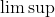
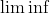
When faced with , think of a sequence of supremums obtained by sequentially chopping off the initial terms of the given sequence. Then take its limit, i.e., its infimum. One can interpret in a similar way.

*Must* use parfor!

I was recently implementing a Monte Carlo simulation with 50000 particles for estimating a probability density function in which took me 1100 seconds of runtime. Using Matlab's profiling tool, I found that 99% of the time was being spent on generating the new set of 50000 sample points from the old sample points. I immediately switched to a parallel looping strategy with 8 workers in parallel. The new runtime dropped to 80 seconds. Next, I found that I was calling a ``coinflip'' function in every loop. I removed it from the loop and instead stored a sequence of coinflips in memory using Matlab's binornd function and simply accessed this vector of ``already flipped coins'' in the parfor. The final runtime was 40 seconds.